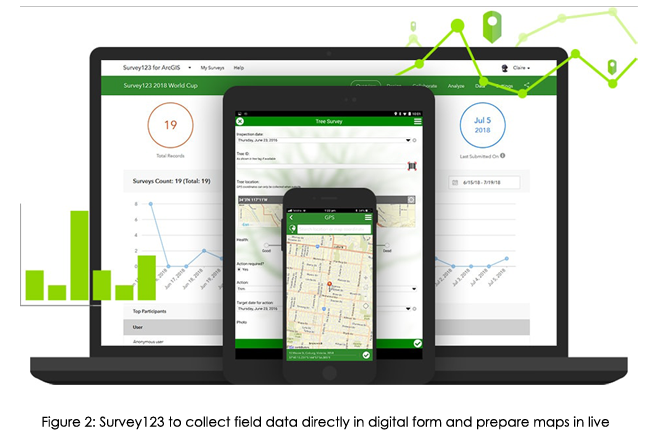
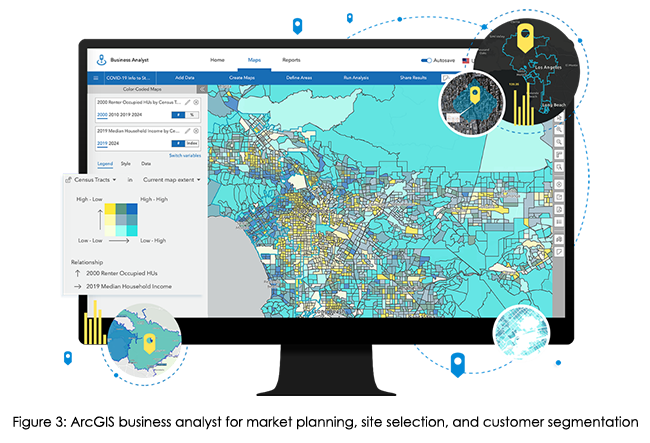
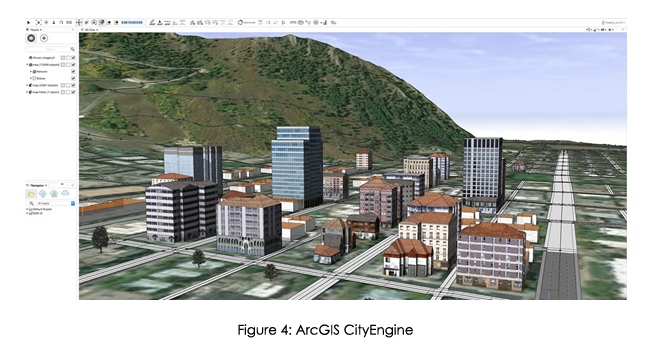
Geographic Information System (GIS) technology has been around for several decades, and it has revolutionized the way we view, analyse, and use geographic data. It is very powerful for managing, analysing, and visualizing spatial data. GIS has evolved significantly in recent years with the introduction of new technologies such as cloud computing, machine learning, and big data analytics. This blog discusses some of the new developments in GIS, the scope of GIS, types of analytics, and future prospects.
New Developments in GIS
In recent years, GIS has seen significant advancements that have transformed the way we collect, manage, analyze and visualize geospatial data. Cloud computing has allowed for more flexible and scalable GIS solutions, while mobile GIS has enabled field workers to access and update geospatial data on-the-go. Machine learning algorithms are being used to extract meaningful insights from large datasets, and big data analytics is helping us to better understand and predict spatial patterns. Additionally, drone-based GIS is revolutionizing data collection, allowing for high-resolution aerial imagery and 3D modelling. Together, these developments are expanding the possibilities for GIS applications across various industries and sectors. Following are the few technologies which are helping GIS technology to accelerate further:
- Cloud Computing: Cloud computing has transformed the way GIS is used by making it possible to store and analyse large amounts of spatial data in the cloud. Cloud computing has also made GIS more accessible to a wider audience, with the advent of cloud-based GIS platforms such as ArcGIS Online, Carto, and Mapbox.
- Mobile GIS: Mobile GIS technology has been around for some time, but recent developments in mobile technology have made it possible to take GIS data into the field, allowing users to collect and update data in real-time. Mobile GIS technology is particularly useful for fieldwork, such as environmental monitoring, asset management, disaster response, and infrastructure maintenance.

- Machine Learning: Machine learning is a type of artificial intelligence that enables computers to learn from data without being explicitly programmed. GIS is now incorporating machine learning algorithms to analyse large amounts of spatial data quickly and accurately, allowing for the identification of patterns, trends, and anomalies.
- Big Data Analytics: With the increasing availability of data from various sources, such as satellite imagery, social media, and sensors, GIS is now using big data analytics to extract meaningful insights from large datasets. Big data analytics has also made it possible to integrate GIS with other data sources, such as business intelligence and customer data.
- Drone-based GIS: Drones equipped with high-resolution cameras and sensors can capture detailed spatial data that was previously impossible to obtain. Drone-based GIS can be used in industries such as agriculture, mining, construction, and environmental monitoring.

Scope of GIS
GIS technology is helping various sectors including environmental management, urban planning, and mining. For environment management, GIS is used to track and monitor changes in land use, water quality, and air pollution, while Mobile GIS allows for on-the-go data collection and cloud computing enables real-time collaboration. Machine learning and big data analytics are used to analyze complex environmental data, improving decision-making. In urban planning, GIS allows for the analysis of population distribution, land use, and infrastructure planning. In mining, drone-based GIS provides high-resolution imagery and 3D modelling, while mobile GIS enables data collection in the field, and machine learning and big data analytics help to locate and assess mineral deposits.
GIS has a wide range of applications across many industries, including:
- Environmental Management: GIS is used for environmental monitoring, natural resource management, and conservation planning. GIS is used to map ecosystems, monitor biodiversity, and track the movement of wildlife.
- Urban Planning: GIS is used in urban planning to map land use, zoning, transportation networks, and utilities. GIS is used to analyse population demographics, predict growth patterns, and identify areas at risk of flooding or other natural disasters.

- Public Health: GIS is used in public health to track disease outbreaks, monitor the spread of diseases, and analyse healthcare needs. GIS is used to map healthcare facilities, track patient data, and analyse health trends.
- Emergency Management: GIS is used to prepare for and respond to disasters in emergency management. GIS is used to map hazards, identify vulnerable populations, and plan evacuation routes.
- Mining: In the mining industry, GIS is used to manage mining operations, monitor environmental impact, and optimize mineral extraction. GIS is used to map geological features, track mineral reserves, and manage mining permits.

- Marketing: GIS is used in marketing to identify target audiences, analyse market trends, and optimize advertising campaigns. GIS helps to map consumer behaviour, analyse spending patterns, and identify new markets.
- Retail: In the retail industry, GIS is used to optimize store locations, analyse foot traffic, and manage supply chains. GIS is used to map consumer demographics, predict sales patterns, and optimize inventory levels.

- Fleet Management: GIS is used in fleet management to optimize routes, reduce fuel consumption, and improve safety. GIS is used to track vehicle location, monitor driver behaviour, and analyse traffic patterns.
Types of GIS Analytics
GIS analytics is a vital component of GIS technology that allows for the extraction of meaningful insights from geospatial data. Together, the below GIS analytics tools provide powerful insights that help decision-makers to better understand spatial patterns and make more informed decisions.
- Spatial Analysis: Spatial analysis is the process of examining spatial data to identify patterns, trends, and relationships. Spatial analysis includes techniques such as clustering, interpolation, and spatial regression.
- Network Analysis: Network analysis is the process of analysing transportation networks, utility networks, and other types of networks. Network analysis includes techniques such as shortest path analysis, travel time analysis, and network optimization.
- Predictive Analytics: Predictive analytics is the process of using historical data to make predictions about future events. Predictive analytics includes techniques such as regression analysis, time-series analysis, and machine learning.

- Real-time Analytics: Real-time analytics is the process of analysing data as it is generated. Real-time analytics is used in applications such as environmental monitoring, traffic management, and disaster response.
- Image Analysis: Image analysis is used to analyse satellite imagery, aerial photography, and other types of imagery. Image analysis tools in GIS can be used to detect changes in land cover, identify land use patterns, and monitor environmental change.
The Evolving Landscape of GIS
GIS technology has come a long way since its inception, and its development shows no signs of slowing down. The combination of new technologies such as cloud computing, machine learning, and big data analytics has made GIS more powerful and accessible than ever before. GIS has a wide range of applications across many industries, and its potential for future growth is huge. As GIS technology continues to evolve, it will undoubtedly lead to new and innovative ways of managing, analysing, and visualizing spatial data.
Some of the future prospects for GIS technology are:
- Increased integration with IoT: GIS is likely to become more integrated with Internet of Things (IoT), which will enable real-time data collection and analysis. This integration will allow GIS to track and analyse data from a variety of sources, including sensors, mobile devices, and social media.
- Increased use of Machine Learning: Machine learning algorithms are expected to become more prevalent in GIS applications, as they enable faster and more accurate analysis of large datasets. Machine learning will be used for tasks such as image classification, pattern recognition, and predictive modelling.
- Greater use of Virtual Reality: Virtual reality (VR) technology is likely to become more integrated with GIS, allowing users to visualize and interact with spatial data in new ways. VR will be used for applications such as urban planning, environmental monitoring, and education.

- Expansion of Cloud-based GIS: Cloud-based GIS platforms will continue to expand, allowing more organizations to access GIS technology without the need for expensive hardware and software. Cloud-based GIS will enable greater collaboration, data sharing, and analysis.
GIS technology is a powerful tool for managing, analysing, and visualizing spatial data. It has a wide range of applications across many industries. The combination of new technologies such as cloud computing, machine learning, and big data analytics has made GIS more powerful and accessible than ever before. As GIS technology continues to evolve, it will undoubtedly lead to new and innovative ways of managing, analysing, and visualizing spatial data. The future of GIS is exciting, and its potential for future growth is vast.